Mogan Gh.L, Butilă E.V., Buzdugan I.D. Proiectarea reductoarelor conico-cilindrice. Universitatea Transilvania din Braşov

Ghid 13.1.2 Verificare arbore intermediar cu cu metode clasice

1. SCHEME DE ÎNCĂRCARE A ARBORELUI INTERMEDIAR

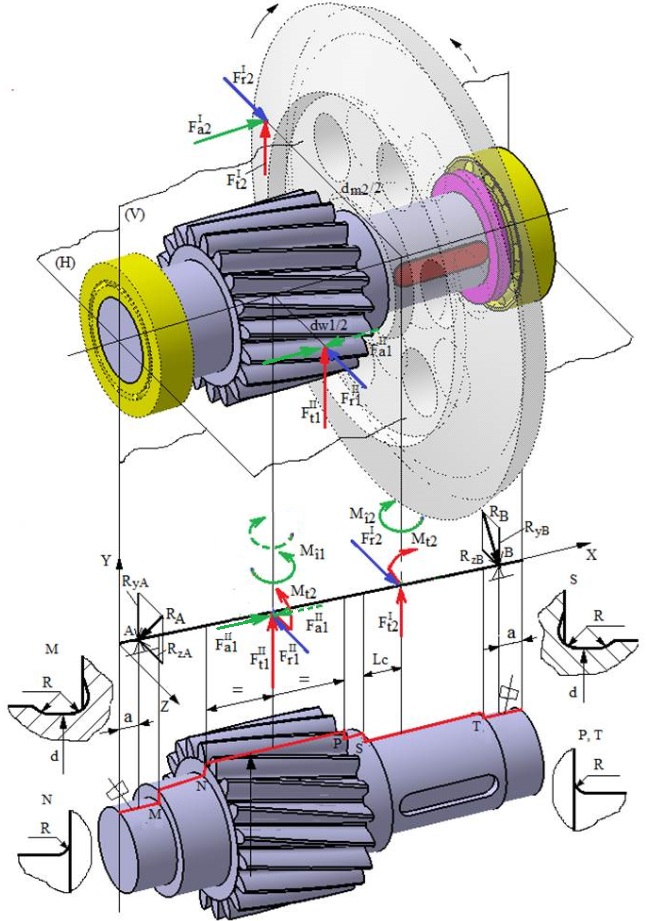
1.1 Schema forţelor de încărcare a arborelui intermediar al RConCil HH

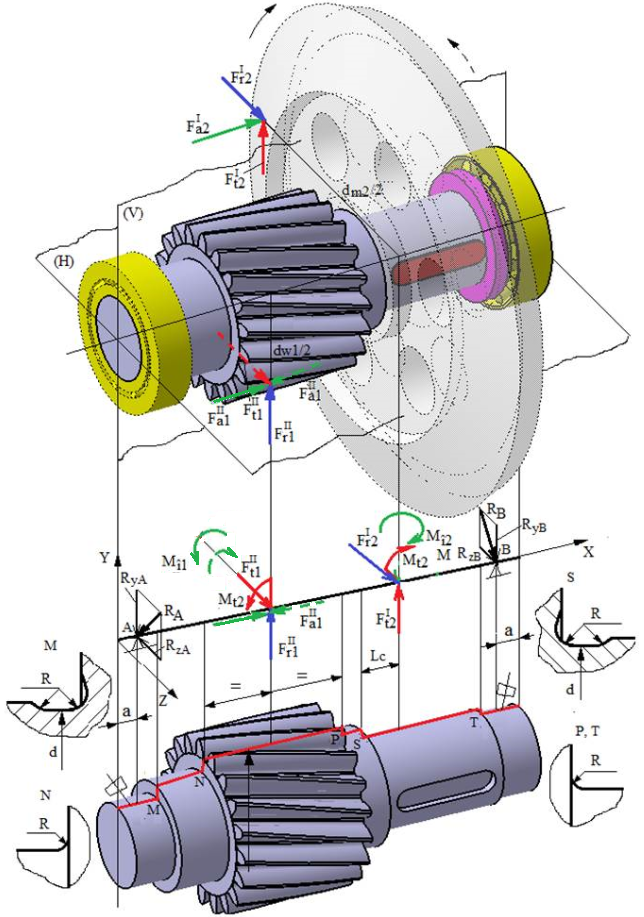
1.2 Schema forţelor de încărcare a arborelui intermediar al RConCil HV

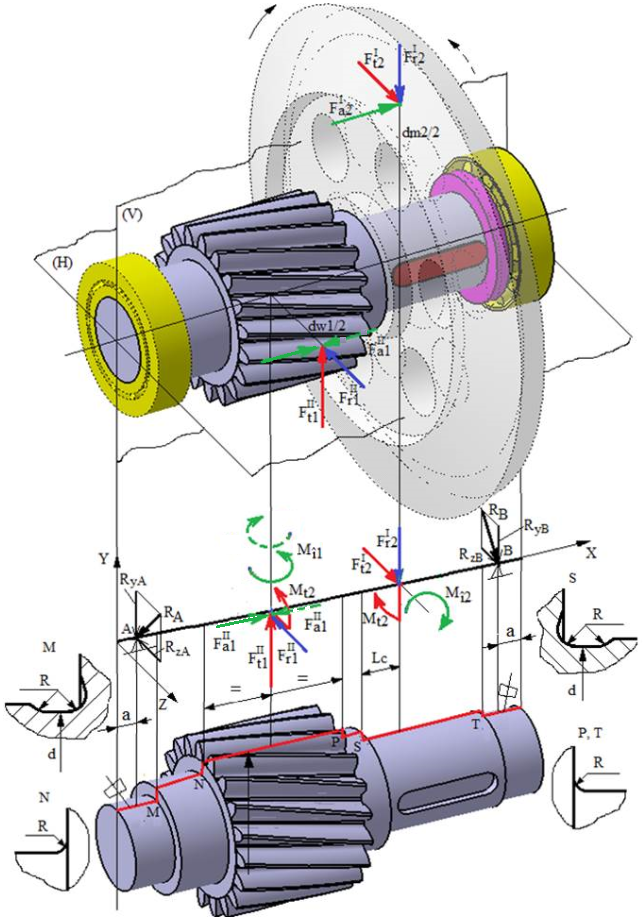
1.3 Schema forţelor de încărcare a arborelui intermediar al RConCil VH

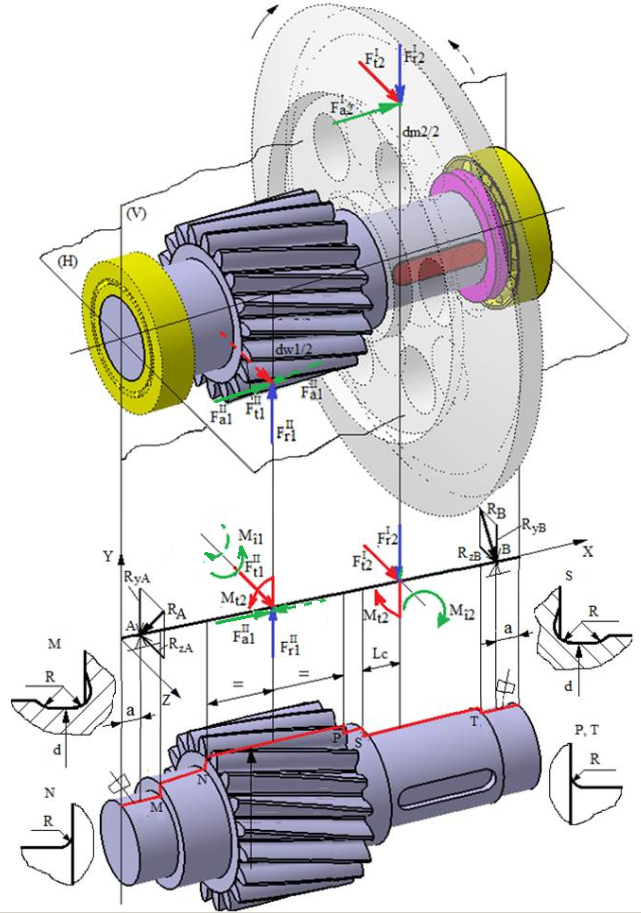
1.4 Schema forţelor de încărcare a arborelui intermediar al RConCil VV

2. DATE DE INTRARE

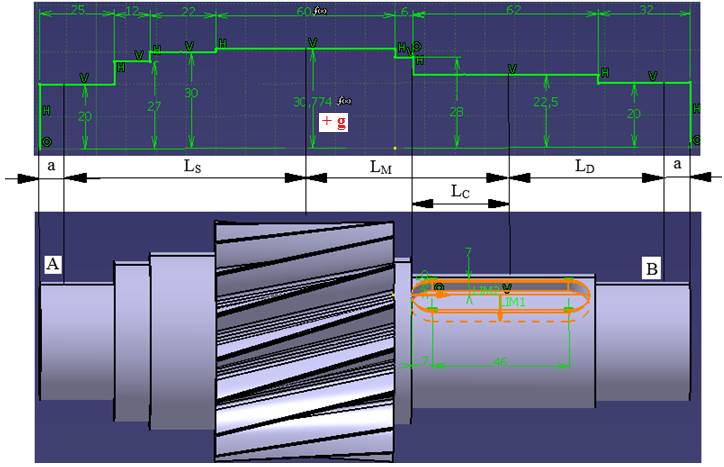
Schema geometriei arborelui conform modelului CATIA

Valori diametre şi lungimi

Diametrele tronsoanelor: conform modelului CATIA.

Lungimi de poziţionare a forţelor şi reacţiunilor:

- L_c, distanţa de la conul suplimentar mediu al roţii conice, unde acţionează forţele din angrenaj (secţiunea mediană), la suprafaţa de rezemarea a acesteia pe arbore (modele de mai sus); se determină prin măsurare din modelul 3D al roţii conice;

- L_S, distanţa de la reazemul A la punctul de acţiune a forţelor pinionului cilindric;

- L_D, distanţa de la reazemul B la punctul de acţiune a forţelor roţii conice;

- L_M, distanţa dintre punctele de acţiune a forţelor pinionului conic şi roţii conice); se determină considerând valoarea L_c;

- a, din catalogul de rulmenţi (Subcap.4.3.1, Ex.4.3) şi L_c, prin măsurare din schiţa CATIA asociată modelul 3D roţii conice;

- g (1 mm), grosimea coroanei dinţate (v. Ghid.9.3).

Valori forţe şi momente

Momentul de torsiune, M_t2 (Ex.2.2).

Forţele de încărcare a roţii conice: tangenţială, ; radială, ; axială, (Ex.7.2).

Forţele de încărcare a pinionului cilindric: tangenţială, ; radială, ; axială, (Ex.7.2).

Momentele de încovoiere (Calc.0):

- M_î2 = d_m2/2 – momentul de încovoire asociat forţei axiale din roata conică,

- M_î1 = d_w1/2 – momentul de încovoire asociat forţei axiale din pinionul cilindric,

pentru valorile diametrelor d_m2 şi d_w1 (v. Ex.6.1.1 şi Ex.6.2.1).

Turația arborelui

n [rot/min], turaţia arborelui intermediar (Ex.2.2).

Date despre material

Tipul oţelului, rezistenţa la rupere şi tratamentul termic (Ex.4.2.1, Anexa.4.2.1.1).

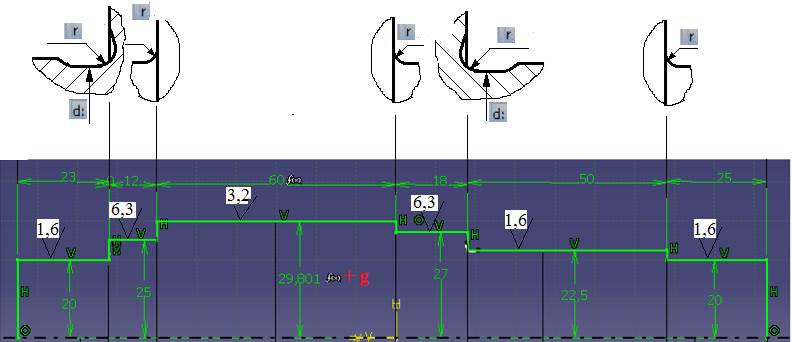
Rezistenţele la oboseală pentru ciclurile alternant simetric şi pulsator: σ_-1, σ₀, τ _-1, τ ₀ (Anexa.4.2.1.2)

Date despre concentratorii de tensiune

3. CALCULUL REACŢIUNILOR DIN RULMENŢI

Determinarea componentelor reacţiunilor din rulmenţi

Tipul reductorului	Relaţii de calcul (conform schemelor de încărcare de mai sus)
	Pentru componentele reacţiuniilor din rulmentul A	Pentru componentele reacţiuniilor din rulmentul B
RCoCil HH	RyA =	RyB =
	RzA =	RzB =
RCoCil HV	RyA =	RyB =
	RzA =	RzB =
RCoCil VH	RyA =	RyB =
	RzA =	RzB =
RCoCil VV	RyA =	RyB =
	RzA =	RzB =
Obs. a. Valorile componentelor reacţiunilor pot rezulta cu + sau cu - (în realitate au sens opus). b. Momentul de încovoiere Mî1, consecinţă a faptului că forţa axială a pionului depinde de sensul de rotaţie a arborelui şi de sensul de înclinare a danturii, poate avea sensuri diferite; în relaţiile de mai sus semnul superior este asociat cu simbolulul cu linie contină, iar semnul inferior simbolului cu linie întreruptă (v. schemele de încărcare. c. Pentru verificarea valorilor componentelor reacţiunilor obţinute mai sus se va verifica relaţiile: + = RyA + RyB, - = RzB - RzA

Determinarea valorilor reacţiunilor din rulmenţi

- R_A = , valoarea reacţiunii din lagărul A,

- R_B = , valoarea reacţiunii din lagărul B.

4. VERIFICAREA ARBORELUI INTERMEDIAR LA SOLICITĂRI COMPUSE

4.1 Verificarea la solicitări compuse a arborelui intermediar HH

Ipoteze de calcul

- se vor considera forţele şi momentele în planele XY şi XZ,

- nu se iau în considerare forţele axiale,

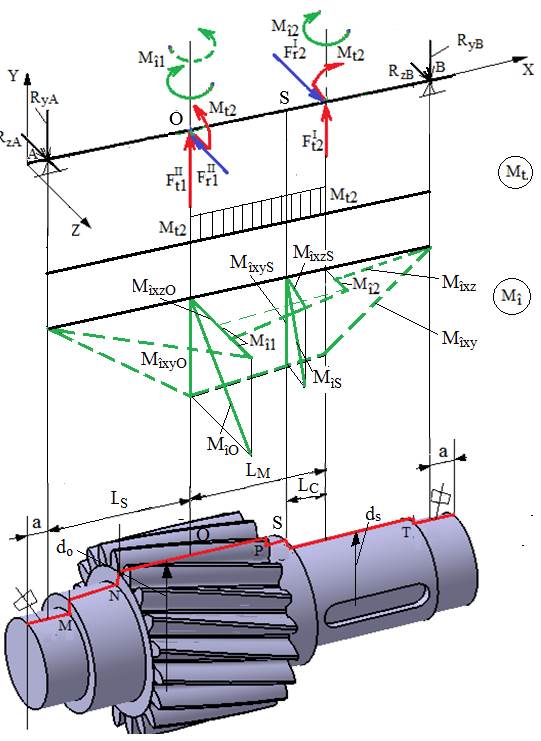
- reprezentarea forţelor se face respectând sensul pozitiv (se va schimba sensul forţelor care au rezultat cu valori negative).

Diagrame de eforturi

- diagrama momentului de torsiune, M_t2, care se menţine constant în zona dintre angrenaje;

- diagramele momentelor de încovoiere:

M_îxz – diagrama momentelor de încovoere din planul XZ, unde:

M_îxzO = R_zA L_S, momentul de încovoiere maxim în planul XZ şi secţiunea O,

M_îxzS = R_zA (L_S + L_M – L_C) - (L_M – L_C) - M_î1, momentul de încovoiere în planul XZ secţiunea S.

M_îxy – diagrama momentelor de încovoere din planul XY, unde:

M_îxyO = R_yA L_S, momentul de încovoiere maxim în planul XY secţiunea O,

M_îxyS = R_yA (L_S + L_M – L_C) - (L_M – L_C), momentul de încovoiere în planul XY secţiunea S.

Determinarea momentelor de încovoiere rezultante

M_îO = , momentul de încovoiere rezultant în secţiunea O,

M_îS = , momentul de încovoiere rezultant în secţiunea S.

Tensiunile echivalente (torsiune şi încovoiere)

- în secţiunea O,

σ_echO = ,

- în secţiunea S,

σ_echS = ,

unde, d_O şi d_S reprezintă diametrele arborelui în secţiunile O şi S (v. subcap. 2), α = σ_aIII/σ_aII – coeficientul diferenţelor dintre ciclurile de încărcare (s-a considerat încărcarea de torsiune pulsatorie, ciclul II); σ_aIII, σ_aII – tensiunile admisibile asociate materialului ales pentru ciclurile de solicitare alternat simetric (III), respectiv, pulsator (II),

conform Anexa 4.2.1.2.

Verificarea la solicitări compuse (torsiune şi încovoiere) a arborelui

σ_echO ≤ σ_aIII,

σ_echS ≤ σ_aIII.

Obs. În cazul neverificării se pot modifica caracteristicile materialului şi/sau valoarea diametrului arborelui.

5. VERIFICAREA ARBORELUI INTERMEDIAR LA SOLICITĂRI VARIABILE (OBOSEALĂ)

Scop şi aspecte generale despre calculul la oboseală

Calculul la solicitări variabile (oboseală), în general, se efectuează în vederea preîntâmpinării ruperii arborilor, cu precădere, în zona concentratorilor de tensiune.

Calculul obişnuit al arborilor la solicitări variabile este de verificare la solicitări (simple sau compuse), de regulă, pentru durabilitate nelimitată (Anexa.13.1.2 Elemente de calcul la solicitări variabile). Acest calcul se face pornind de la o diagrama rezistenţelor la oboseală (a ciclurilor limită a materialului pentru care se adoptă o diagramă schematizată, simplificată (Sodeberg, Goodman, Serensen), pe baza căreia se stabilesc relaţii de calcul pentru coeficientul de siguranţă, ca raportul dintre rezistenţa la oboseală a materialului (tensiunea maximă a ciclului limită) şi tensiunea maximă a ciclului de solicitări variabile.

Verificarea la solicitări variabile

Condiţia rezistenţei la oboseală a arborilor drepţi în zonele care există concentratori de tensiuni (canale de pană, caneluri, salturi de diametre, găuri transversale, filet, ajustaje presate etc.), cu precădere, supuşi la solicitări compuse (torsiune şi încovoiere) este dată de relaţia,

c ≥ c_a,

ce presupune calculul în zonele cu concentratori de tensiune a coeficientului de siguranţă global,  ,  

c =   ,          

care se determină în funcţie de coeficienţii de siguranţă parţiali (conform schematizării simplificată, Serensen),                 

c_σ =  ,                       

c_τ = ,        

în care,  σ_-1, τ_-1 sunt rezistenţa la oboseală pentru solicitarea de încovoiere, respectiv torsiune, pentru ciclul alternant simetric; τ₀ – rezistenţa la oboseală pentru solicitarea de torsiune, pentru ciclul pulsator; τ_m – tensiunea medie a ciclului de solicitare la torsiune; σ_v, τ_v – amplitudinile ciclurilor de solicitare la încovoiere, respectiv la torsiune; β_kσ, β_κτ - coeficienţi de concentrare a tensiunilor în secţiunea considerată, corespunzători solicitării de încovoiere, respectiv de torsiune; ε_σ, ε_τ - coeficienţi dimensionali, corespunzători solicitării de încovoiere, respectiv de torsiune; γ_σ, γ_τ - coeficienţi de calitate a suprafeţelor, corespunzători solicitării de încovoiere, respectiv de torsiune.

Pentru coeficientul de siguranţă admisibil, se recomandă valorile: c_a = 1,3 ... 1,5 – pentru arbori executaţi din material omogen, cu solicitări precis stabilite; c_a = 1,5 ... 2,5 – pentru arbori executaţi din material neomogen şi la care solicitările sunt stabilite cu aproximaţie.

Coeficienţii β_kσ, β_κτ, γ_σ, γ_τ, ε_σ, ε_τ (Anexa.13.1.4) introduc corecţii care ţin seama de faptul că încercările la oboseală ale materialelor se fac pe epruvete standard care se execută fără concentratori de tensiuni şi ale căror dimensiuni şi prelucrări diferă de cele ale arborilor proiectaţi.

Obs.

În cazul în care într-o anumită secţiune condiţia impusă prin relaţia de verificare nu este îndeplinită, se iau măsuri constructive pentru îndeplinirea ei prin introducerea de concentratori care induc tensiuni locale mult reduse (Anexa.13.1.3).